Data Mining And Business Intelligence (2170715)

BE | Semester-7   Winter-2018 | 03/12/2018

Q2) (c) 

Explain Mean, Median, Mode, Variance, Standard Deviation & five number summary with suitable database example.

  • Mean
    • Mean is the average of a dataset.
    • To find the mean, calculate the sum of all the data and then divide by the total number of data
    • Example : Find out mean for 12, 15, 11, 11, 7, 13
      • First, find the sum of the data. : 12 + 15 +11 + 11 + 7 + 13 = 69
      • Then divide by the total number of data. : 69 / 6 = 11.5
      • Therefore, Mean = 11.5
  • Median
    • Median is the middle number in a dataset when the data is arranged in numerical order (Sorted Order).
    • If count is Odd then middle number is Median
    • If count is Even then take average of middle two numbers that is Median
    • Example : Find out Median for 12, 15, 11, 11, 7, 13, 15
      • In above example, count of data is 7. (Odd)
      • First, arrange the data in ascending order. : 7, 11, 11, 12, 13, 15, 15
      • Partitioning data into equal halfs 7, 11, 11, 12, 13, 15, 15
      • Therefore, The Median = 12
  • Mode
    • The mode is the number that occurs most often within a set of numbers.
    • Example : Find mode. : 12, 15, 11, 11, 7, 13
    • As 11 is repeated maximum time, Mode = 11
  • Standard Deviation
    • The Standard Deviation is a measure of how spread out any data are.
    • Its symbol is s (the Greek letter sigma)
    • Sample Variance : (s)2 = 1/(π - 1 ) Σi=1n(x - mean)2
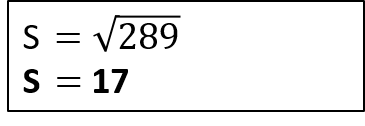
    • Standard Deviation is Square root of sample variance.
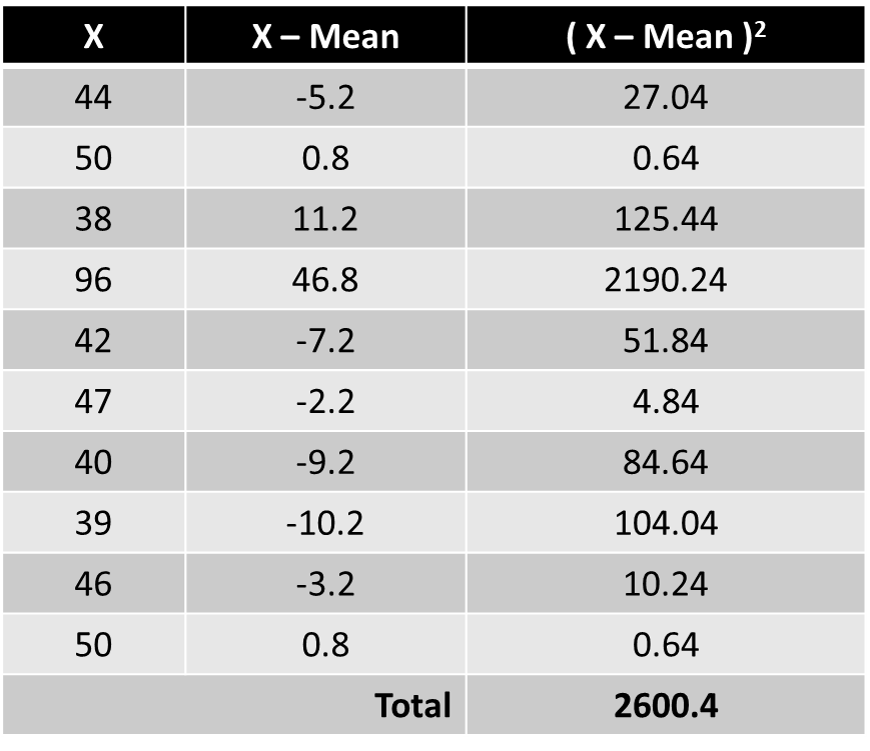
    • Example : The owner of the Indian restaurant is interested in how much people spend at the restaurant.
      He examines 10 randomly selected receipts for parties and writes down the following data. : 44, 50, 38, 96, 42, 47, 40, 39, 46, 50
      • Ans :
        1. Find out Mean
          • Mean is 49.2
        2. Write a table that subtracts the mean from each observed value. table
        3. table
        4. table

Questions

Go to Question Paper