Explain collision in the context of hashing? Discuss collision resolution techniques.
What is Hashing?
- Sequential search requires, on the average O(n) comparisons to locate an element, so many comparisons are not desirable for a large database of elements.
- Binary search requires much fewer comparisons on the average O (log n) but there is an additional requirement that the data should be sorted. Even with best sorting algorithm, sorting of elements require O(n log n) comparisons.
- There is another widely used technique for storing of data called hashing. It does away with the requirement of keeping data sorted (as in binary search) and its best case timing complexity is of constant order O(1). In its worst case, hashing algorithm starts behaving like linear search.
- Best case timing behavior of searching using hashing = O(1)
- Worst case timing Behavior of searching using hashing = O(n)
Collision Resolution Strategies
- Collision resolution is the main problem in hashing.
- If the element to be inserted is mapped to the same location, where an element is already inserted then we have a collision and it must be resolved.
- There are several strategies for collision resolution. The most commonly used are :
- Separate chaining - used with open hashing
- Open addressing - used with closed hashing
Separate chaining
- In this strategy, a separate list of all elements mapped to the same value is maintained.
- Separate chaining is based on collision avoidance.
- If memory space is tight, separate chaining should be avoided.
- Additional memory space for links is wasted in storing address of linked elements.
- Hashing function should ensure even distribution of elements among buckets; otherwise the timing behaviour of most operations on hash table will deteriorate.
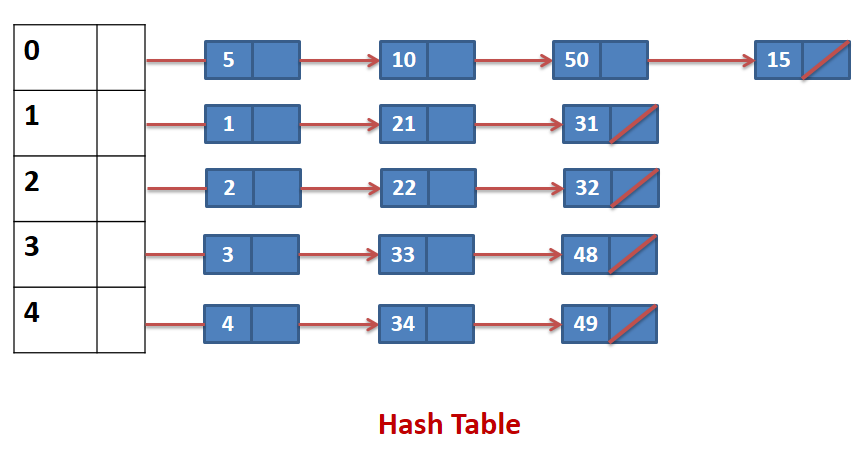
- Example : The integers given below are to be inserted in a hash table with 5 locations using chaining to resolve collisions. Construct hash table and use simplest hash function.
1, 2, 3, 4, 5, 10, 21, 22, 33, 34, 15, 32, 31, 48, 49, 50
- An element can be mapped to a location in the hash table using the mapping function key % 10
| HASH TABLE LOCATION |
MAPPED ELEMENTS |
| 0 |
5, 10, 15, 50 |
| 1 |
1,21,31 |
| 2 |
2,22,32 |
| 3 |
3,33,48 |
| 4 |
4,34,49 |
Open Addressing
- Separate chaining requires additional memory space for pointers. Open addressing hashing is an alternate method of handling collision.
- In open addressing, if a collision occurs, alternate cells are tried until an empty cell is found.
- Linear probing
- Quadratic probing
- Double hashing.
a) Linear Probing
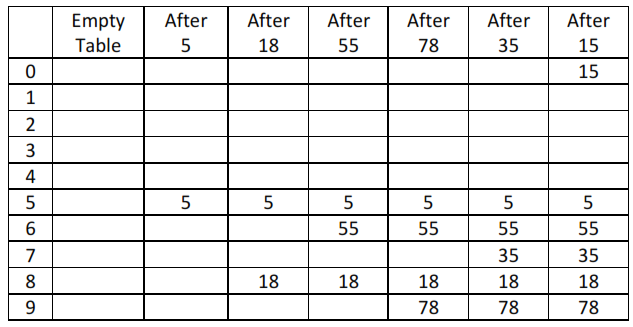
- In linear probing, whenever there is a collision, cells are searched sequentially (with wraparound) for an empty cell.
- Fig. shows the result of inserting keys {5,18,55,78,35,15} using the hash function (f(key)= key%10) and linear probing strategy.
- Linear probing is easy to implement but it suffers from "primary clustering".
- When many keys are mapped to the same location (clustering), linear probing will not distribute these keys evenly in the hash table. These keys will be stored in neighborhood of the location where they are mapped. This will lead to clustering of keys around the point of collision.
b) Quadratic probing
- One way of reducing "primary clustering" is to use quadratic probing to resolve collision.
- Suppose the "key" is mapped to the location j and the cell j is already occupied. In quadratic probing, the location j, (j+1), (j+4), (j+9), ... are examined to find the first empty cell where the key is to be inserted.
- This table reduces primary clustering.
- It does not ensure that all cells in the table will be examined to find an empty cell. Thus, it may be possible that key will not be inserted even if there is an empty cell in the table.
c) Double Hashing
- This method requires two hashing functions f1 (key) and f2 (key).
- Problem of clustering can easily be handled through double hashing.
- Function f1 (key) is known as primary hash function.
- In case the address obtained by f1 (key) is already occupied by a key, the function f2 (key) is evaluated.
- The second function f2 (key) is used to compute the increment to be added to the address obtained by the first hash function f1 (key) in case of collision.
- The search for an empty location is made successively at the addresses f1 (key) + f2(key), f1 (key) + 2f2 (key), f1 (key) + 3f2(key),...