Discuss different representations of a graph.
Representation of Graph
- A diagrammatic representation of a graph may have limited usefulness. However such a representation is not feasible when number of nodes an edges in a graph is large.
- Hence the graph can be represented in another two ways.
- Matrix representation of Graph
- Linked List representation of Graph
Matrix Representation of Graph (Adjacency matrix)
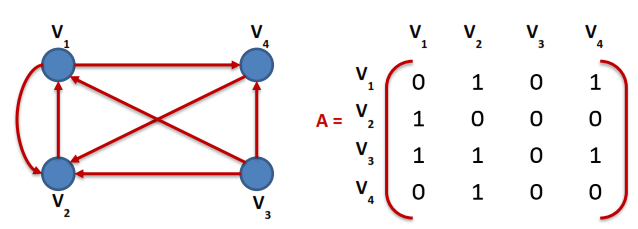
- The number of elements in the ith row whose value is 1 is equal to the out-degree of node Vi.
- The number of elements in the jth column whose value is 1 is equal to the in-degree of node Vj.
- For a NULL graph which consist of only n nodes but no edges, the adjacency matrix has all its elements 0. i.e. the adjacency matrix is the NULL matrix.
Linked List representation of Graph (Adjacency List Representation)