Theory Of Computation (2160704)

Moore Machine

• Mathematically Moore machine is a six tuple machine and defined as M₀=(Q,Σ,Δ,δ,Λ^',q₀)
  Where,
  • Q : a nonempty finite set of states in M₀
  • Σ : a nonempty finite set of input symbols
  • Δ : a nonempty finite set of outputs
  • δ : Transition function which takes two arguments as in finite automata, one is input state and other is input symbol. The output of this function is a single state.
  • λ^': it is a mapping function which maps Q to Δ, giving the output associated with each state.
  • q₀ : the initial state of M₀ and q₀ ∈ Q
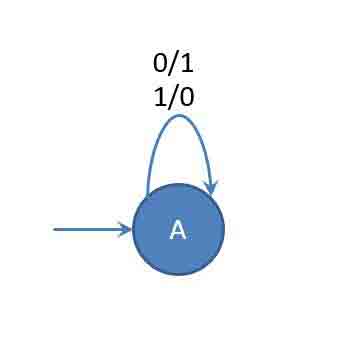
• Example : Design a moore machine for the 1’s compliment of binary number.

Mealy Machine

• Mathematically Mealy machine is a six tuple machine and defined as M_e=(Q,Σ,Δ,δ,λ^',q₀)
  Where,
  • Q : a nonempty finite set of states in M_e
  • Σ : a nonempty finite set of input symbols
  • Δ : a nonempty finite set of outputs
  • δ : Transition function which takes two arguments as in finite automata, one is input state and other is input symbol. The output of this function is a single state.
  • λ^': It is a mapping function which maps Q×Σ to Δ, giving the output associated with each transition.
  • q₀ : the initial state of M_e and q₀ ∈ Q
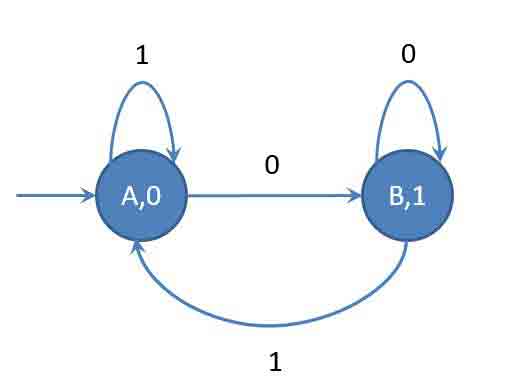
• Example : Design a mealy machine for the 1’s compliment of binary number