Explain push down automata with example and their application in detail
Pushdown Automata
-
A pushdown Automata (PDA) is a 7-tuple M = (Q,Σ,Γ, q0,Z0,A,δ),
where
-
Q is finite set of states
Σ and are finite sets of i/p symbol
Γ is stack alphabet
??0 the initial state, is an element of Q
Z0 the initial stack symbol, is an element of Γ
A is a set of accepting states, is a subset of Q
δ : Q × (Σ ∪ {^}) × Γ -> the set of finite subsets of Q × Γ*
The function δ is called transition function of M.
-
Example : Design PDA for L={anbn/a,b∈Σ,n≥0} or PDA for Number of a’s and b’s are same.
| Move No |
State |
i/p |
Stack Symbol |
Move |
| 1 |
q0 |
^ |
Z0 |
(q2,z0) |
| 2 |
q0 |
a |
Z0 |
(q0,aZ0) |
| 3 |
q0 |
a |
a |
(q0,aa) |
| 4 |
q0 |
b |
a |
(q1,^) |
| 5 |
q1 |
b |
a |
(q1,^) |
| 6 |
q1 |
^ |
Z0 |
(q2,Z0) |
| Resulting State |
Unread i/p |
Stack |
| q0 |
aaabbb |
Z0 |
| q0 |
aabbb |
aZ0 |
| q0 |
abbb |
aaZ0 |
| q0 |
bbb |
aaaZ0 |
| q1 |
bb |
aaZ0 |
| q1 |
b |
aZ0 |
| q1 |
^ |
Z0 |
| q2 |
^ |
Z0 |
|
|
accepted |
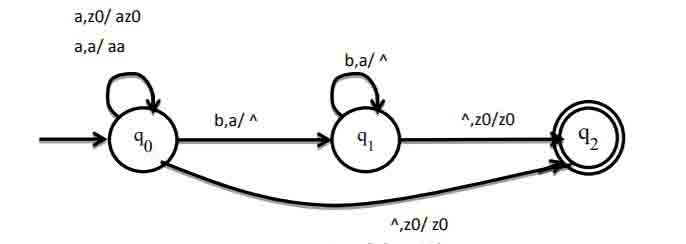
(Figure: PDA accepting Number of a’s and b’s are same)
Applications Of Pushdown Automata
-
A pushdown automata is a way to implement a context free grammar.
-
PDA is used in parser design for syntactic analysis.